NEWS
2023年6月17日

蒙特卡罗：蒙特卡洛 Monte Carlo 入门（15分钟版）

蒙特卡洛 Monte Carlo 入门（15分钟版）

20世纪40年代，蒙特卡洛（Monte Carlo, 位于摩纳哥的赌城，如标题图）方法由John von Neumann，Stanislaw Ulam和 Nicholas Metropolis 在 Los Alamos National Lab (LANL) 曼哈顿计划中，为模拟中子扩散发展出的一种统计方法。 正如名字反映出的，蒙特卡洛方法本质上是跟赌博一样具有随机特性。

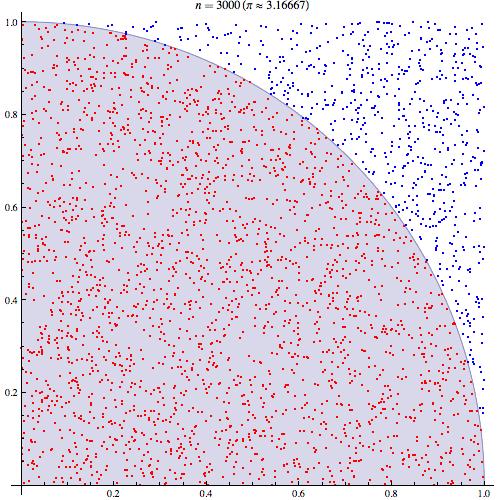
如果(x,y)是独立地从0到1之间均匀分布抽样出的一系列的数对number pair, 那么这些随机的位置坐标(x,y)落在1为半径圆弧内的概率应该是：四分之一圆的面积➗整个正方形的面积：

蒙特卡罗P= \frac{\rm Area\; of\; circle}{\rm Area\; of \;square} = \frac{\pi r^2/4}{1} = \frac{\pi}{4}

而因为(x,y) 是0到1的均匀分布，所以这个概率当抽样足够多的时候就等于红色的点数除以总共点数：

P=\frac{\# Red}{\# Total}= \frac{\pi}{4} \;\; \Rightarrow \pi \approx \frac{4\;\; \# Red}{\# Total}

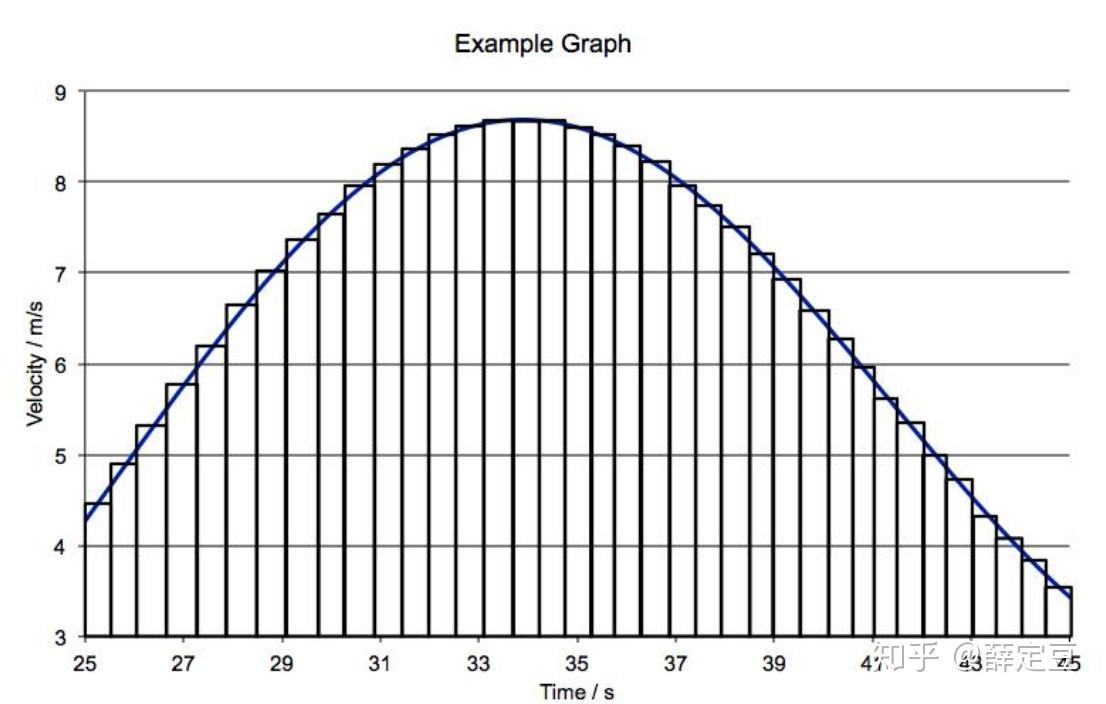
这样一来，只要采样足够多，就可以得到无限趋近于\pi的值。这个例子很好的体现了Monte Carlo（MC)方法的精神：利用随机分布的特性，大数次抽样得到准确的估计。换句话说，就是我猜，我猜地又多又均匀就基本上成功了！

微积分里我们学到，定积分（也就是曲线下的面积）可以想象成很多等宽小矩形加起来的面积之和，如下图所示，

I= \int_a^b dx f(x) = \sum_{i=1}^N f(x_i) \Delta x

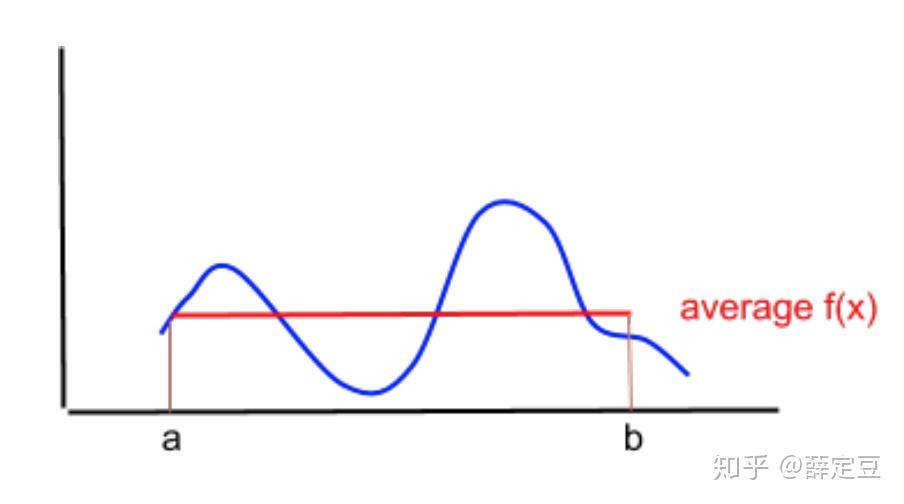
如果用蒙特卡洛的思维来做的话，可以从a到b的均匀分布产生一些列的x值： \{x_i\},i=1,\ldots,N ，只要抽样足够多，就可以估计出在这个区间内 f(x) 的平均值，记做 \langle f(x) \rangle 这样一来，曲线下面积就等效成一个以这个平均值为高的矩形面积：

蒙特卡罗：蒙特卡洛 Monte Carlo 入门（15分钟版）

I = \int_a^b dx f(x) = (b-a)\frac{\sum_{i=1}^N f(x_i)}{N} = (b-a) \langle f(x) \rangle

其实，很多积分中 f(x) 还是有一些重要的区域的，为了使采样更有效率，一般我们可以采用重要性抽样来计算积分：

I=\int_a^b dx f(x) = \int_a^b dx \rho(x) \frac{f(x)}{\rho(x)} = \int_a^b dx \rho(x) g(x) \approx \frac{1}{N} \sum_{i=1}^N g(x_i)

这里， \rho(x) 是任意满足正定 \rho(x)> 0 且归一化 \int dx \rho(x)=1 条件的概率分布，且 \{x_i\} 是从这个分布采样的随机数。重要性抽样其实仅仅就是做了个恒等变形，把原来要均匀采样的概率分布（其实就是 \rho(x)=\frac{1}{b-a}\;\mathrm{for\;all} \;\;a\le x<b ）替换成任意概率分布，并把要平均的函数除以这个分布。重要性抽样是统计和物理中常见的方法，可以很好的对重点区域采样而快速估计积分。

另一方面，重要性抽样有着很简单直接的并行化方案：对于多维定积分， \mathbf x=(x_1,x_2,\ldots,x_P) 从分布 \rho(x_1,x_2,\ldots,x_P) 中采样的话，（这里为了符号简便，现在暂时将第 i 次采样记做带括号的上标 ^{(i)} ）

I = \int d x_1 \int dx_1\cdots \int dx_P f(x_1,x_2,\ldots,x_P) \equiv\int d \mathbf x f(x_1,x_2,\ldots,x_P) \\= \int d\mathbf x\rho(x_1,x_2,\ldots,x_P) \left[\frac{f(x_1,x_2,\ldots,x_P)}{\rho(x_1,x_2,\ldots,x_P)} \right] \\ =\frac{1}{N} \sum_{i=1}^N \left[\frac{f(x_1^{(i)},x_2^{(i)},\ldots,x_P^{(i)})}{\rho(x_1^{(i)},x_2^{(i)},\ldots,x_P^{(i)})} \right]\\ =\frac{1}{N} \sum_{i=1}^N \left[\frac{f(\mathbf x^{(i)})}{\rho(\mathbf x^{(i)})} \right] = \frac{1}{N} \sum_{i=1}^N g(\mathbf x^{(i)})

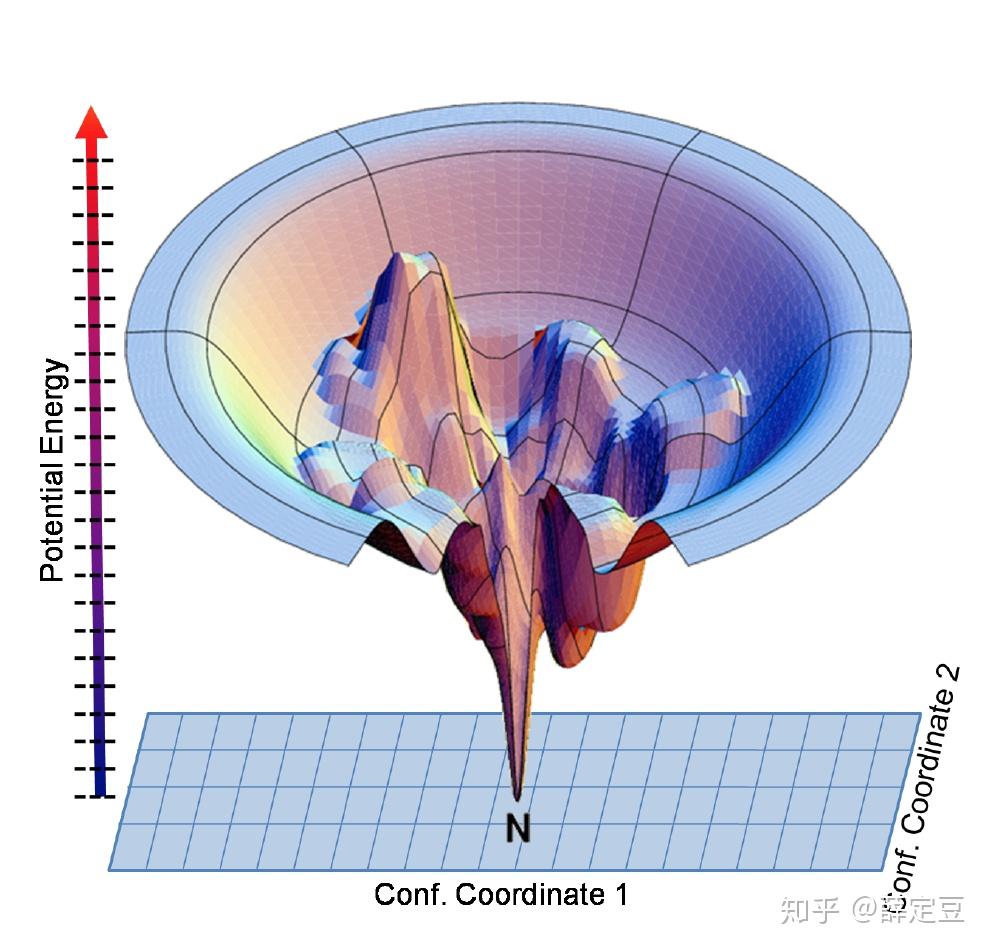
其实，统计力学里常见的积分就是物理量 A 的系综平均

\langle A \rangle = \int d\mathbf x\rho (\mathbf x) A(\mathbf x) = \frac{1}{N}\sum_{i=1}^N A(\mathbf x^{(i)})

这里\rho(\mathbf x) = \frac{1}{Z} e^{-\beta H(\mathbf x)} 是正则系综分布函数， Z=\int d\mathbf x e^{-\beta H(\mathbf x)} 是正则配分函数。

那么，问题来了，怎么对任意分布 \rho(\mathbf x) 采样？这里介绍Metropolis MC算法，也叫Metropolis-Hastings算法，它类似于随机瞎走（Random walk）的方式产生一列数，这些数的总体分布服从 \rho(\mathbf x) 。这里，我们以平衡态统计力学中的最常见的Boltzmann分布为例说明。

玻尔兹曼分布说对于构型 \mathbf x_a ,它的概率应该是 P_a \propto e^{-\beta E_a} ,这里 E_a = H(\mathbf x_a) 是这个构型的能量。我们想要产生服从玻尔兹曼分布的一系列 \mathbf x ,可以设想如果我基于原来的一个构型 \mathbf x_a 怎么产生下一个构型 \mathbf x_b 呢？

当体系达到平衡时，体系在 \mathbf x_a 的概率 P_a 不应该随时间改变，于是有

\frac{d}{dt}P_a = \sum_b \left[ w_{b \to a} P_b - w_{a\to b} P_a\right]=0

这里 w_{a\to b} 表示基于 \mathbf x_a 随机产生 \mathbf x_b 的转移概率（Transition probability），求和是对于所有可能的其他构型\mathbf x_b。从上面关系可以得到只要满足下面细致平衡（detailed balance)条件，就可以产生出服从玻尔兹曼分布的序列：

\frac{w_{a\to b}}{w_{b \to a}} = \frac{P_b}{P_a} = e^{-\beta(E_b - E_a) } = e^{\beta \Delta E_{ab}}

Metropolis选择的是下面方式选择转移概率（尽量最大化接受新构型）：

w_{a\to b} =\left\{ \begin{array}{cc} e^{\beta \Delta E_{ab}} & (E_b > E_a) \\ 1 & (E_b \le E_a)\end{array}\right.

w_{b\to a} =\left\{ \begin{array}{cc} 1& (E_b > E_a) \\ e^{-\beta \Delta E_{ab}} & (E_b \le E_a)\end{array}\right.

读者可以将上面两个式子相除，就可以看出在不管新构型的能量是更高还是更低，这个转移概率的比值都服从细致平衡条件，也就是最终产生的分布就会使玻尔兹曼分布了。

Metropolis算法——移动然后选择接受这个移动还是拒绝这个移动

  1. 从起始构型 \mathbf x^{(i)} ，计算能量 E^{(i)} ；
  2. 随机移动一些构型坐标得到一个trial构型 \mathbf x^{(i+1')} ，并计算该构型的能量 E^{(i+1')} ；
  3. 决定是否接受这个移动：
    （1）如果 E^{(i+1')}\le E^{(i)} ,那么100%接受这个移动，正式的下一步构型就是 \mathbf x^{(i+1)} =\mathbf x^{(i+1')} 了；
    （2）如果 E^{(i+1')}> E^{(i)} ,那么产生一个0到1之间的随机数R, 并跟转移概率 w_{i\to i+1'} = \exp(\beta \Delta E_{i,i+1'}) 比较，如果 w_{i\to i+1'} > R 那就接受这个移动 \mathbf x^{(i+1)} =\mathbf x^{(i+1')} ，否则就拒绝这个移动 \mathbf x^{(i+1)} =\mathbf x^{(i)} ；
  4. 回到第二步，直到累积N个构型。

这一列构型 \mathbf x^{(1)},\mathbf x^{(2)},\mathbf x^{(3)},\ldots,\mathbf x^{(N)} 被称为马尔科夫链(Markov Chain)，因为产生的新构型只跟当前构型有关，对前面的构型没有任何的记忆效应，所以这个方法又叫马尔科夫链蒙特卡洛（MCMC）。而且，从任何初始构型出发，最终都会达到平衡而且服从就是玻尔兹曼分布，即通过配比转移概率 w_{a \to b} 达到对某构型的采样概率为P_a \propto e^{-\beta E_a} 且不随“时间”改变。【注意：MC里序列是没有物理上时间先后关系的，所有说MC“时间序列”都是指随机产生的顺序。】

当然，这个例子只是一个统计力学里的概率分布函数，其实任何形式的分布都可以用MC产生，使得MC方法在统计里应用的不要太多。

谢谢！

Potential 蒙特卡罗 Energy Landscape

相关文章 :